Blackbody Radiation

References

• “Modern Physics”, Serway

The success of Maxwell’s theory led to attempts to use it to solve the mystery of Blackbody radiation. The problem is in predicting the radiation intensity at a given wavelength, $I$ v.s. $\lambda$, emitted by a hot glowing solid at a specific temperature T. In the late 1700s Thomas Wedgewood, a relative to Charles Darwin and renowned China maker, noticed that the object in his oven all glowed red at a the same temperature. With the use of spectroscopy in the mid-1800s, it was shown that the emissions were continuous instead of discrete.

Kirchoff’s contribution

In 1859 Gustav Kirchoff proved a theorem using thermodynamics that for any body in thermal equilibrium with radiation the emitted power is proportional to the power absorbed

$$e_f=J(f,T)A_f$$

With $e_f$ being the power emitted per unit area per unit frequency by a particular heated object, $A_f$ is the absorption power (fraction of the incident power absorbed per unit area per unit frequency by the heated object), and $J(f,T)$ which is a universal function (same for all objects) that depends only on the light frequency $f$, and the absolute temperature of the body $T$. A blackbody is defined as an object that absorbs all the electromagnetic radiation falling on it and consequently appears black. It has $A_f=1$ for all frequencies and Kirchoff’s theorem for a blackbody becomes

$$e_f=J(f,T)$$

which says that the power emitted per unit area per unit frequency is independent of chemical composition and only depends on frequency and temperature, in agreement with Wedgewoods observations. Because absorption and emission is connected via Kirchoff’s theorem, we see that a blackbody is a perfect absorber and ideal radiator. In practice, a small opening in any cavity, such as a port in an oven, behaves like a blackbody because the opening traps all incoming radiation. The radiation emmited out of a port is in thermal equilibrium with the walls because it has been absorbed and re-emitted many times.

Stefan’s contribution

The next important contribution came from Josef Stefan (1835 - 1893) an Austrian Physicist, in 1879. He found experimentally that the total power per unit area emitted at all frequencies by a hot solid, $e_{total}$, was proportional to the fourth power of its absolute temperature. Therefore Stefan’s law may be written as

$$e_{total}={\int }_0^{\infty }{e}_{f}df=\sigma T^4$$

where $\sigma$ is the Stefan-Boltzmann constant, given by $\sigma =5.67\times 10^{-8}$ $\mathrm{W}\cdot {\mathrm{m}}^{-2}\cdot {\mathrm{K}}^{-4}$. A body that is not an ideal radiator will obey the same general expression but with a coefficient, a, that is less than one.

$$e_{total}=a\sigma T^4$$

5 years later Boltzmann confirmed Stefan’s Law using electromagnetic and thermodynamic arguments. Another triumph of Maxwell’s theory.

Example of Stefan’s Law and the Sun

Estimate the surface temperature of the Sun from the following information. The Sun’s radius is given by $R_s=7.0\times 10^8$ m . The average Earth-Sun distance is $R=1.5\times 10^{11}$ m. The power per unit area (at all frequencies) from the Sun is measured at the Earth to be 1400 $W/{\mathrm{m}}^2$. Assume the Sun is a blackbody.

Solution: For a blackbody we take $a=1$, so

$$e_{total}(R_s)=\sigma T^4$$

where $e_{total}(R_s)$ stand for the total power per unit area at all frequencies at the surface of the Sun. Because the problem gives the total power per unit area at the Earth, $e_{total}(R)$, we need to connect this to $e_{total}(R_S)$. This comes from conservation of energy

$$e_{total}(R_S)\cdot 4\pi R_s^2=e_{total}(R)\cdot 4\pi R^2$$ $$e_{total}(R_S)=e_{total}(R)\cdot \frac{R^2}{R_S^2}$$

Then using Stefan’s formula

$$T=(\frac{e_{total}(R_s)}{\sigma }{)}^{1/4}=(\frac{e_{total}(R)\cdot R^2}{\sigma R_S^2}{)}^{1/4}$$

Plugging in the known values we get

$$T=5800\mathrm{K}$$

Wien’s Contribution

As can be seen in figure 1, the wavelength of the maximum power emission of a blackbody, ${\lambda }_{max}$ shifts to shorter wavelengths with increasing temperature. This agrees with Wedgewood’s observations that objects in his kiln progressed from dull red to orange to white as the temperature got hotter. The simple effect of ${\lambda }_{max}\propto T^{-1}$, was not definitively established, however, until about 20 years after Kirchoff’s seminal paper had started the search to find the universal function J(f, T). in 1893, Wilhelm Wien proposed a general form for the blackbody distribution law, J(f, T) that gave correct experimental behavior of ${\lambda }_{max}$ with temperature. This is called Wien’s displacement law and is written as

$${\lambda }_{max}T=2.898\times 10^{-3}\mathrm{m}\cdot \mathrm{K}$$

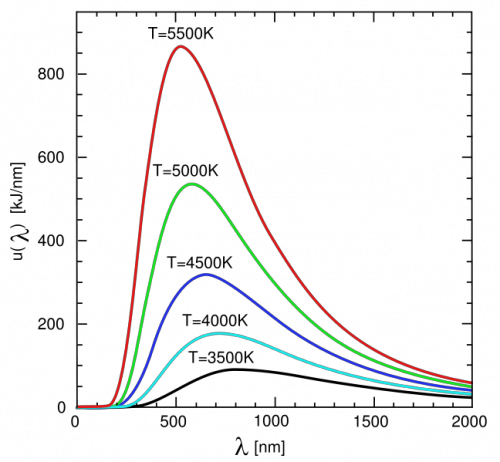
Assuming that the peak sensitivity of the human eye (which occurs at around 500 nm - blue-green light) coincides with ${\lambda }_{max}$ for the Sun (a blackbody), we can check the consistency of Wien’s displacement law with Stefan’s law by recalculating the Sun’s surface temperature:

$$T=\frac{2.898\times 10^{-3}\mathrm{m}\cdot \mathrm{K}}{500\times 10^{-9}\mathrm{m}}=5800\mathrm{K}$$

So far we have discussed the power radiated per unit area per unit frequency by the black body, J(f,T). However, it is more convenient to consider the spectral energy density, which is the energy per unit volume per unit frequency of the radiation within the blackbody cavity, $u(f,T)$. For light in equilibrium with the cavity walls, the power emitted per square centimeter of opening is simply proportional to the energy density of the light inside the cavity. Because the light is isotropic and unpolarized, one can average over direction to show the constant of proportionality between $J(f,T)$ and $u(f,T)$ is $c/4$, where $c$ is the speed of light. Therefore

$$J(f,T)=u(f,T)c/4$$

An important guess to the form of the universal function, $u(f,T)$, was made in 1893 by Wien and had the form

$$u(f,T)=A{f}^3{e}^{-\beta f/T}$$

where A and $\beta$ are constants. This was known as the Wiens exponential law, it resembles and is loosely based on Maxwell’s velocity distribution for gas molecules. Within a year, the German spectroscopist Friedrich Paschen had confirmed Wein’s guess by working in the then difficult range of 1 to 4 $\mu$m and at temperatures 400 to 1600 K.

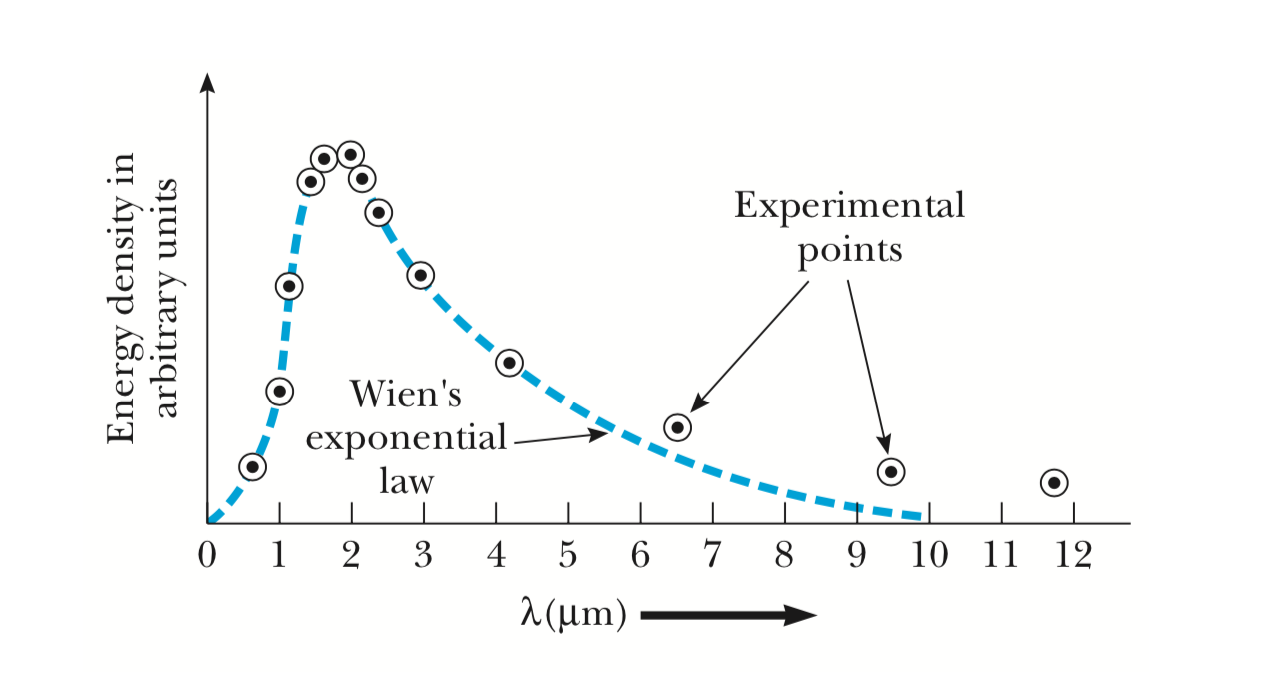
As can be seen in the figure, Paschen made most of his measurements in the maximum energy region of a body heated to 1500 K and had found good agreement with Weins law. In 1900 however, Lummer and Pringsheim extended the measurements to 18 $\mu$m, and Rubens and Kurlbaum went even further - 60 $\mu$m. Both teams concluded that Wein’s Law failed in this region

Planck’s Contribution

On a Sunday evening in October of 1900, Max Planck discovered the famous Blackbody formula, which truly ushered in Quantum-Mechanics quantum theory. Planck’s proximity to the Reichsensalt experimentalists was extremely important to his discovery - earlier in the day he had heard from Rubens that his latest measurements showed that $u(f,T)$, the spectral energy density, was proportional to T for long wavelengths or low frequency. Planck knew that Wein’s law worked well for smaller wavelengths (higher frequency) and indeed had been working hard to derive Wein’s laws from principles of statistical mechanics and Maxwell’s equations. Interpolating between the two limiting forms (Wein’s exponential law and an energy density proportional to temperature), he immediately found a general formula, which he send to Rubens on a postcard in the same evening. His formula was

$$u(f,T)=\frac{8\pi h{f}^3}{c^3}(\frac{1}{e^{hf/k_{B}T}-1})$$

where h is Planck’s constant = $6.626\times 10^{-34}\mathrm{J}\cdot \mathrm{s}$, and $k_B$ is Boltzmann’s constant = $1.380\times 10^{-23}J/K$. This has the correct limiting behavior at high and low frequencies with the help of a few approximations.

At high frequencies $hf/k_{B}T>>1$,

$$\frac{1}{e^{hf/k_{B}T}-1}\approx e^{-hf/k_{B}T}$$

and

$$u(f,T)\approx \frac{8\pi h{f}^3}{c^3}{e}^{-hf/k_{B}T}$$

and we recover Wein’s exponential law.

At low frequencies, $hf/k_{B}T<<1$,

$$\frac{1}{e^{hf/k_{B}T}-1}=\frac{1}{1+\frac{hf}{k_{B}T}+\cdots +-1}\approx \frac{k_{B}T}{hf}$$

and

$$u(f,T)\approx \frac{8\pi f^2}{c^3}{k}_{B}T$$

This shows that the energy is proportional to T in the low-frequency or so called classical region as Rubens had found.