Perturbation Theory

References

• “Quantum Mechanics”, David McIntyre

Real problems are rarely exactly solvable as in the case of particle in a box, harmonic oscillator and Hydrogen atom. The goal is then to model real problems as perturbations to the exactly solvable systems. We assume that the perturbation is small so that we can use approximations to find the corrections to the exact solutions. The focus is to find the corrections to the energies and eigenstates.

Spin-1/2 Example

The Hamiltonian of a spin-1/2 system is the potential energy of the spin magnetic moment in an applied magnetic field. For an applied magnetic field in the z-direction $\mathbf{B}=B_0\hat{\mathbf{z}}$ the Hamiltonian is

$$H_0=-\mu \cdot \mathbf{B}={\omega }_0{S}_z=\frac{\hslash }{2}\left(\begin{array}{cc}{\omega }_0& 0\\ 0& -{\omega }_0\end{array}\right)$$

where the Larmor frequency is ${\omega }_0=e{B}_0/m_e$. The subscript zero indicates that this is the zeroth-order Hamiltonian. The energy eigenstates of the zeroth-order Hamiltonian are the spin up and down states $|\pm ⟩$ and the energy eigenvalues are

$$E_{\pm }^{(0)}=\pm \frac{\hslash {\omega }_0}{2}$$

where the superscript zero on the energy denotes the order of the solution. The goal of perturbation theory is to find the higher-order corrections to the energy eigenvalues and eigenstates caused by the spplication of a perturbation to the system.

The simplest way to perturb the spin system is to change the magnetic field. Any general change to the magnetic field can be decomposed into an additional component along the original field in the z-direction and an additional component perpendicular to that. We write the new total field as $\mathbf{B}=B_0\hat{\mathbf{z}}+B_1\hat{\mathbf{z}}+B_2\hat{\mathbf{x}}$ and characterize the two additional field components by their respective Larmor frequencies ${\omega }_1=e{B}_1/m_e$ and ${\omega }_2=e{B}_2/m_e$. With this notation, the new Hamiltonian is

$$H=-\mu \cdot \mathbf{B}={\omega }_0{S}_z+{\omega }_1{S}_z+{\omega }_2{S}_x=\frac{\hslash }{2}\left(\begin{array}{cc}{\omega }_0+{\omega }_1& {\omega }_2\\ {\omega }_2& -{\omega }_0-{\omega }_1\end{array}\right)$$

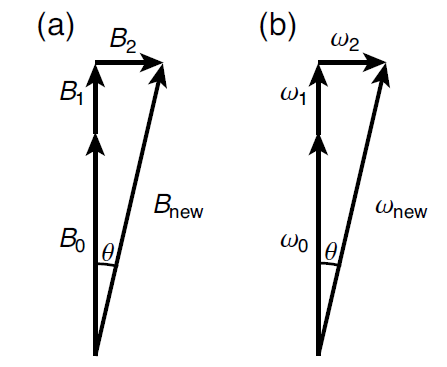
(a) Perturbing magnetic fields and (b) the resultant Larmor frequencies

It is useful to separate the new Hamiltonian into the zeroth-order Hamiltonian $H_0$ and the perturbation Hamiltonian that we denote $H^{{}^{\prime }}$

$$H=H_0+H^{{}^{\prime }}$$

The zeroth-order Hamiltonian is given previously and the perturbation Hamiltonian is

$$H^{{}^{\prime }}=\frac{\hslash }{2}\left(\begin{array}{cc}{\omega }_1& {\omega }_2\\ {\omega }_2& -{\omega }_1\end{array}\right)$$

The perturbation Hamiltonian has terms along the diagonal and terms off the diagonal. These play important roles in perturbation theory.

We now solve the energy eigenvalues and eigenstates of the new Hamiltonian exactly by diagonalizing the matrix. But we have already done this in chapter 2 for the general spin-1/2 case of a magnetic field at an angle $\theta$ to the z-axis. We found there that the Hamiltonian is proportional to the spin component $S_n$ along the new magnetic field direction $\hat{\mathbf{n}}$, and can be expressed in terms of the angel $\theta$ of the new field as

$$H={\omega }_{new}{S}_n=\left(\begin{array}{cc}\cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array}\right)$$

where $\theta ={\tan }^{-1}(\frac{{\omega }_2}{{\omega }_0+{\omega }_1})$ and the new Larmor frequency obeys the Pythagorean equation

$${\omega }_{new}=\sqrt{({\omega }_0+{\omega }_1{)}^2+{\omega }_2^2}$$

corresponding to the total field. The eigenstates of this new Hamiltonian are the spin states ${|\pm ⟩}_n$ aligned along or against the new field and the eigenenergies are

$$E_{new}=\pm \frac{\hslash }{2}=\pm \frac{\hslash }{2}\sqrt{({\omega }_0+{\omega }_1{)}^2+{\omega }_2^2}$$

This is the exact solution, which we now expand as a power series.

We assume that the added fields are small in comparison to the original field which implies that the new Larmor frequencies ${\omega }_1$ and ${\omega }_2$ are small compared to the original Larmor frequency. Hence, we treat the ratios ${\omega }_1/{\omega }_0$ and ${\omega }_2/{\omega }_0$ of the new to old Larmor frequencies as small dimensionless parameters and rewrite the energy in the previous equation as

$$E_{new}=\pm \frac{\hslash {\omega }_0}{2}\sqrt{(1+\frac{{\omega }_1}{{\omega }_0}{)}^2+\frac{{\omega }_2^2}{{\omega }_0^2}}$$ $$E_{new}=\pm \frac{\hslash {\omega }_0}{2}\sqrt{1+\frac{2{\omega }_1}{{\omega }_0}+\frac{{\omega }_1^2}{{\omega }_0^2}+\frac{{\omega }_2^2}{{\omega }_0^2}}$$

So far this is still the exact solution. Now we expand the exact energy to second order in a power series (Taylor series about $x=0$ where $x=\frac{2{\omega }_1}{{\omega }_0}+\frac{{\omega }_1^2}{{\omega }_0^2}+\frac{{\omega }_2^2}{{\omega }_0^2})$ in the small parameters ${\omega }_1/{\omega }_0$ and ${\omega }_2/{\omega }_0$, so as to reach some general conclusions about perturbation theory:

$$E_{new}=\pm \frac{\hslash {\omega }_0}{2}[1+\frac{2{\omega }_1}{{\omega }_0}+\frac{{\omega }_1^2}{{\omega }_0^2}+\frac{{\omega }_2^2}{{\omega }_0^2}{]}^{1/2}$$ $$E_{new}=\pm \frac{\hslash {\omega }_0}{2}[1+\frac{{\omega }_1}{{\omega }_0}+\frac{{\omega }_1^2}{2{\omega }_0^2}+\frac{{\omega }_2^2}{2{\omega }_0^2}-\frac{1}{8}(\frac{2{\omega }_1}{{\omega }_0}+\frac{{\omega }_1^2}{{\omega }_0^2}+\frac{{\omega }_2^2}{{\omega }_0^2}{)}^2+\cdots ]$$ $$E_{new}\approx \pm \frac{\hslash {\omega }_0}{2}[1+\frac{{\omega }_1}{{\omega }_0}+\frac{{\omega }_2^2}{2{\omega }_0^2}]$$

We conclude that the two energies of the the perturbed system, to second order in the small quantities characterizing the perturbation, are

$$E_{+}\approx +\frac{\hslash {\omega }_0}{2}+\frac{\hslash {\omega }_1}{2}+\frac{\hslash {\omega }_2^2}{4{\omega }_0}$$ $$E_{-}\approx -\frac{\hslash {\omega }_0}{2}-\frac{\hslash {\omega }_1}{2}-\frac{\hslash {\omega }_2^2}{4{\omega }_0}$$

In both energies, we identify the first term as the zeroth-order energy $E_{\pm }^{(0)}$, and note two additional terms. The first is linear or first order in the perturbation and is equal to the corresponding diagonal term $\pm \hslash {\omega }_1/2$ in the Perturbation Hamiltonian. The second term is quadratic or second order in the perturbation and is proportional to the square of the off-diagonal term $\hslash {\omega }_2/2$ in the perturbation Hamiltonian. The general pattern of corrections is characteristic of perturbation theory, so we denote perturbed energies as the series

$$E_n=E_n^{(0)}+E_n^{(1)}+E_n^{(2)}+\cdots$$

where the superscript indicates the order of the perturbation. The energies quadratic dependence on the off-diagonal terms of the Perturbation Hamiltonian and linear dependence on the diagonal terms of the perturbation Hamiltonian is a general feature of perturbation theory. The second order correction has a factor of ${\omega }_0$ in the denominator, and it will diverge if the energy splitting $\hslash {\omega }_0$ is zero, (i.e, if the original levels are degenerate in energy). This divergence violates the assumption that the perturbation corrections are small, which creates a problem that will be addressed in degenerate perturbation theory.

The eigenstates also exhibit corrections. The eigenstates of the full Hamiltonian are the spin up and down eigenstates ${|\pm ⟩}_n$ along the direction $\hat{\mathbf{n}}$: ${|+⟩}_n=\cos \frac{\theta }{2}|+⟩+\sin \frac{\theta }{2}|-⟩$ ${|-⟩}_n=-\sin \frac{\theta }{2}|+⟩+\cos \frac{\theta }{2}|-⟩$ The angle $\theta$ is small for small perturbing magnetic field, so we can also us $\theta$ as a small parameter for a series expansion ${|+⟩}_n\approx (1-\frac{{\theta }^2}{8})|+⟩+\frac{\theta }{2}|-⟩=|+⟩+\frac{\theta }{2}|-⟩-\frac{{\theta }^2}{8}|+⟩$ ${|-⟩}_n\approx -\frac{\theta }{2}|+⟩+(1-\frac{{\theta }^2}{8})|-⟩=|-⟩-\frac{\theta }{2}|+⟩-\frac{{\theta }^2}{8}|-⟩$ To the second order in the angle $\theta$, the new eigenstates have two correction terms: a first-order term that is orthogonal to the original state, and a second-order term that is parallel (in a Hilbert space sense, not a geometric sense) to the original state. If we neglect the parallel terms (see later why we do this, my guess is normalization), we get:

$${|+⟩}_n\approx |+⟩+\frac{\theta }{2}|-⟩$$

${|-⟩}_n\approx |-⟩-\frac{\theta }{2}|+⟩$ Expressing the small angle in terms of the Larmor frequencies, to first order we obtain

$$\theta \approx \frac{{\omega }_2}{\sqrt{({\omega }_0+{\omega }_1{)}^2+{\omega }_2^2}}\approx \frac{{\omega }_2}{{\omega }_0}$$

Thus we arrive at the perturbation series expansion for the perturbed states, to first order

$${|+⟩}_n\approx |+⟩+\frac{{\omega }_2}{2{\omega }_0}|-⟩$$

${|-⟩}_n\approx |-⟩-\frac{{\omega }_2}{2{\omega }_0}|-⟩$ We conclude that the first-order eigenstate correction depends only on the off-diagonal matrix element, not on the diagonal elements. Note that the coefficient of the original state remains one, which makes it appear that the state is no longer normalized. But if we check the normalization of the perturbed state, we will find that it is normalized to first order approximation.