Anyons

Anyons have fractional statistics and charge, and are thought to be a possible ingredient in the creation of topological quantum computers. By braiding their world lines, the non-Abelian exchange statistics can encode quantum information.

Fractional Statistics and Charge

• Bosons even upon exchange $P\Psi (x_1,x_2)=\Psi (x_2,x_1)$
• Fermions odd upon exchange $P\Psi (x_1,x_2)=-\Psi (x_2,x_1)$
• Anyons have fractional statistics upon exchange $P\Psi (x_1,x_2)=e^{i\theta }\Psi (x_2,x_1)$

Timeline

“Quantum Mechanics of Fractional-Spin Particles”, Frank Wilczek (1982)

• Composites formed from charged particles and vortices in (2+1)-dimensional models, or flux tubes in three-dimensional models, can have any (fractional) angular momentum
• The statistics of these objects, like their spin, interpolates continuously between the usual boson and fermion cases.
• Although practical applications of these phenomena seem remote, I think they have considerable methodological interest and shed light on fundamental spin-statistics connection

“Statistics of Quasiparticles and the Hierarchy of Fractional Quantized Hall States”, Bertrand Halperin (1983)

• Appearance of fractional statistics

“Fractional Statistics and the QHE”, Arovas, Schrieffer, Wilczek (1984)

• Statistics if quasiparticles entering the QHE are deduced from the adiabatic theorem
• Excitations found to obey fractional statistics, related to their fractional charge

Fractional Quantum Hall Effect

• IQHE have plateaus at integer filling $\nu =n$, $n\in \mathbb{Z}$
• Plateaus and fractional filling $\nu =p/q$ where $p/q$ is a rational fraction
• Quasi particles carry fractional charge $e\ast =\nu e$
• Braiding statistics ${\theta }_{anyon}=2\pi \frac{e^{\ast }}{e}$

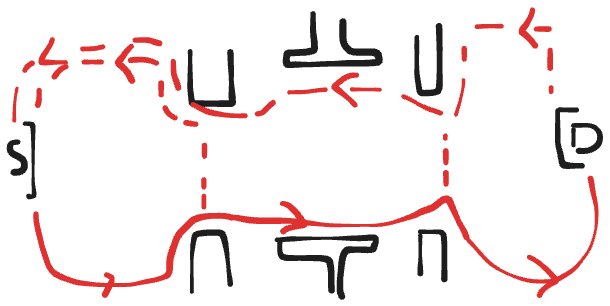
Fabry-Perot Interferometry

A square interference region bounded by two QPCs serving as beam splitters. Two bound anyons in the interference region introduces a phase shift.

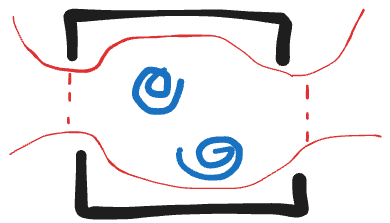
Surface gates define electron interference path (plungers)

The current is

$$I\propto |t_1{|}^2+|t_2{|}^2+|t_1||t_2|\cos \theta$$

In integer QHE phase

$$\theta =2\pi \frac{AB}{{\varphi }_0}$$

where ${\varphi }_0=\frac{h}{e}$. In FQHE phase

$$\theta =2\pi \frac{AB}{{\varphi }_0}\frac{e}{e^{\ast }}+N_L{\theta }_{anyon}$$

We expect to see phase slips if there is an anyon bound within the interference region

Problem: Strong bulk-edge coupling will shrink effective area of interference region via Coulomb interaction with edge mode and bound charges. This will result in lines of positive barber shop pole slope in $\beta \delta V$ versus $BA/{\Phi }_0$

This coupling effect can result in different regimes (Aharanov Bohm $\to$ Coulomb) depending on the stiffness

• Occurs in small devices (increasing charging energy)
• Increasing size goes toward AB regime, but lose coherence

Solution: Sandwich 2DEG between capacitor (screening well heterostructure with top and bottom gating) $\to$ quench charging energy

Now, strong and highly coherent AB interference in integer and fractional regimes observed

3D Anyons

Intersections of vortex loops in disordered Weyl semimetal with atomic planes are anyons