References

• Berry Phases in Electronic Structure Theory, David Vanderbilt

Orbital Magnetization

The Polarization $\mathbf{P}$ and magnetization $\mathbf{M}$ are electric and magnetic order parameters that couple to external electric and magnetic fields

The spontaneous magnetization (in absence of external magnetic field) has two components, one coming from spin, and the other the orbital motion of the electrons

• $\mathbf{M}={\mathbf{M}}_{spin}+{\mathbf{M}}_{orb}$

In most ferromagnetic materials, ${\mathbf{M}}_{spin}$ is typically dominant. This is because of the excess spin up or spin down electrons in the valence bands.

The orbital contribution ${\mathbf{M}}_{\mathbf{orb}}$ arises from circulating currents from the orbital motion of the electrons on the atoms in the crystal. This is typically induced by a spin-orbit coupling term in the Hamiltonian on a given atomic site $H_{SOC}=\xi \mathbf{L}\cdot \mathbf{S}$ (largest for heavier atoms).

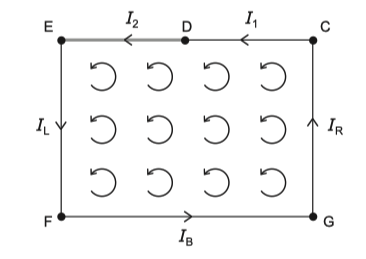
Finite Systems

The orbital magnetization gives rise to surface current ${\mathbf{K}}_{surf}=c{\mathbf{M}}_{orb}\times \hat{n}$ on the edges of the sample. For a finite system such as an atom or molecule, the orbital magnetic dipole moment is calculated as

$$\mathbf{m}=\frac{1}{2c}\int \mathbf{r}\times \mathbf{j}(\mathbf{r})d^{3}r$$

Bulk systems

In bulk systems, the modern theory of polarization tells us that $\mathbf{P}$ is only defined as a bulk quantity modulo a quantum. This is because an adiabatic change to the surface can change the occupancy of the surface states, changes the bound charge, and consequently, the bulk polarization.

The orbital magnetization, ${\mathbf{M}}_{orb}$, on the other hand, is uniquely defined in the conventional sense. Conservation of charge requires the edge current to be constant, otherwise this is not a stationary state since charge accumulates. We can’t change the surface current by any local changes to surface.

Naively, the bulk orbital magnetization in a magnetic crystal could be,

$$\mathbf{M}=\frac{1}{2c{V}_{cell}}{\int }_{cell}\mathbf{r}\times \mathbf{j}(\mathbf{r})d^{3}r$$

where the integral in over the interior of the unit cell. However, this will depend on the choice of unit cell. Even perfect knowledge of the periodic bulk $\mathbf{j}$ is insufficient for determining the orbital magnetization (Hirst, 1997).

In almost all ferromagnetic materials, the orbital current are associated with partially filled $d$ or $f$ shells of magnetic atoms. These are localized, and can construct set of non-overlapping atomic spheres around magnetic ions and approximate $\mathbf{M}$ as the sum over their contributions.

We would like a proper definition of orbital magnetization that applies to time-reversal broken systems where orbital currents extend into bonding regions between atoms, or even flowing along paths between atoms.

Quantum Expression

We need a quantum mechanical expression. For a finite system like an atom or molecule, the expression is

$$\mathbf{m}=\frac{-e}{2c}\sum _{n\in occ}⟨{\psi }_n|\mathbf{r}\times \mathbf{v}|{\psi }_n⟩$$

where $\mathbf{v}$ is the velocity operator. For a crystal, the position operator is ill defined in Bloch representation. Analogous to the modern theory of polarization, we can hope to express it in terms of a Berry connection.

An approach based on Wannier representation put forth by Thonhauser (2005) and Ceresoli (2006). A semiclassical theory proposed by Xiao (2005). A long-wave perturbation analysis Shi (2007). They all arrive at (in 2D)

$$M=\frac{e}{\hslash c}\frac{1}{(2\pi {)}^2}\sum _n{\int }_{BZ}\text{Im}⟨{\partial }_x{u}_{n\mathbf{k}}|H_{\mathbf{k}}+E_{n\mathbf{k}}-2E_F|{\partial }_y{u}_{n\mathbf{k}}⟩f_{n\mathbf{k}}{d}^{2}k$$

where ${\partial }_u=\partial /\partial k_{\mu }$. The term involving $E_F$ is proportional to the total Chern number for an insulator, and can be dropped for trivial insulators.

In 3D, ${\mathbf{M}}_{orb}$ is a pseudovector, giving rise to a 2D surface sheet current ${\mathbf{K}}_{surf}={\mathbf{M}}_{orb}\times \hat{n}$ for surface normal $\hat{n}$. We can simply average over wavevectors in spectator directions. For magnetization, this leads to the 3D formula

$$M_{\alpha }=\frac{e}{2\hslash c}\frac{1}{(2\pi {)}^3}\sum _n{\int }_{BZ}\text{Im}{ϵ}_{\alpha \mu \nu }⟨{\partial }_{\mu }{u}_{n\mathbf{k}}|H_{\mathbf{k}}+E_{n\mathbf{k}}-2E_F|{\partial }_{\nu }{u}_{n\mathbf{k}}⟩d^{3}k$$

We can also write it as

$$\mathbf{M}=\frac{e}{2\hslash c}\frac{1}{(2\pi {)}^3}\sum _n{\int }_{BZ}\text{Im}⟨{\nabla }_{\mathbf{k}}{u}_{n\mathbf{k}}|\times H_{\mathbf{k}}+E_{n\mathbf{k}}-2E_F|{\nabla }_{\mathbf{k}}{u}_{n\mathbf{k}}⟩d^{3}k$$

For a review see Thonhauser (2011) and Hanke et al. (2016)

Ambiguity modulo a quantum?

Polarization in 1D constrains the surface charge $Q_{surf}$ modulo a charge quantum $e$. If we want to know the $P_x$ component in 2D or 3D, connected to edge or surface charges, then we use the 1D Berry-phase theory in the $x$ direction and average over wavevectors in other “spectator” directions.

Orbital magnetization first arises in 2D, since there are no circulating currents in 1D. $M_{orb}$ is a pseudoscalar (invariant under inversion but odd under TR) that determines the edge current $I$. This time there is no ambiguity modulo a quantum. The edge current is $I=M_{orb}$ independent of edge conditions.

Wannier Derivation

Multiband generalization

• gauge invariance: Souza, Vanderbilt (2008)
• f-sum rule: Yao et al. (2008)

Applications

• Thonhauser (2011)
• Hanke (2016)