Topological Crystalline Insulators

References

• Alexander Altland and Martin R. Zirnbauer. Non-standard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B, 55:1142–1161, Jan 1997.
• Barry Bradlyn, L. Elcoro, Jennifer Cano, M. G. Vergniory, Zhijun Wang, C. Felser, M. I. Aroyo, and B. Andrei Bernevig. Topological quantum chemistry. Nature, 547, 2017.
• Jennifer Cano, Barry Bradlyn, Zhijun Wang, L. Elcoro, M. G. Vergniory, C. Felser, M. I. Aroyo, and B. Andrei Bernevig. Building blocks of topological quantum chemistry: Elementary band representations. Phys. Rev. B, 97:035139, Jan 2018.
• Liang Fu. Topological crystalline insulators. Phys. Rev. Lett., 106:106802, Mar 2011.

Topological insulators, such as the Chern insulator and ${\mathbb{Z}}_2$ insulator, are characterized by their gapless surface states and $K$-theoretic topological invariants. In these familiar cases, crystalline symmetries do not play a role. However, in some instances, crystalline symmetries may be crucial in determining and protecting the topological phase. Insulators whose topological phase depends on crystal symmetries are called topological crystalline insulators (TCIs).

Crystal Symmetries

Point Groups are a set of lattice operations that leaves at least one point invariant. Some possible operations are

• Rotation: Leaves entire axis invariant
• Mirror: Leaves entire plane invariant
• Inversion: Leaves the origin invariant
• Roto-inversion: rotation plus inversion

For example, the $T_d$ point group consists of a $C_4$ rotation operation $\times$ inversion, but not either one individually. A point group combined with translation generates a space group. In 3D, there are 14 possible Bravais lattices generated by translation operations. Combined with all the possible point groups, there are 230 possible space groups, not including magnetic symmetries which are another story.

Symmetries in the Hamiltonian

A system is said to have a symmetry if its Hamiltonian commutes with that particular symmetry operation. This block-diagonalizes the Hamiltonian according to its symmetries. For example, translation symmetry allows us to block-diagonalize the Hamiltonian in k-space. Crystal symmetries can mix different k-space blocks. At a general k-point, the Hamiltonian does not commute with the crystal symmetry operations.

A symmetry operation has a matrix representation $\Delta (G)$ , where $G$ is the element of the symmetry group. This describes how it acts on our Hilbert space. The Hamiltonian transforms under the symmetry element as $\Delta (G)H(k)\Delta (G)=H(Gk)$ Notice the the crystal momentum is also transformed. Each $k$ has associated with it a “little group” consisting of the subset of crystal symmetry operations that leave it invariant $G{k}_0=k_0$. The energy bands at $k_0$ can be classified as representations of the little group. This means that the eigenstates of each band at $k_0$ can be given a label corresponding to representations of the little group of that $k_0$.

Going from any point along a high-symmetry line, the symmetry of the line is generically lower than the symmetry of the point, and will be a subgroup of the little group. Knowing the symmetry of a point, you can uniquely figure out the representation along the line by decomposing the representation of the little group at $k_0$ into representations of the little group along the line. This generates compatibility relations that tell you how the points and lines can connect with each other. These compatibility relations are a cornerstone to the theory of topological quantum chemistry.

Tenfold Way

The tenfold way, or the Altland-Zirnbauer classification, distinguishes systems according to their symmetry class and dimension, restricting the possible values the topological invariant can take. These symmetry classes correspond to systems with or without a combination of time-reversal, particle-hole, and chiral (sublattice) symmetries. Some possible classes are

• Class A in 2d: $\mathbb{Z}$ invariant
  • No symmetry
  • Integer quantum Hall / Chern insulator
• Class AII in 2d and 3d: ${\mathbb{Z}}_2$ invariant
  • Time reversal symmetry present (for spin 1/2 fermions)
  • Describes topological insulators
    • Weak indices not captured.

However this table only depends on the internal symmetries of the system. For example, the weak indices in a topological insulator depends on translational symmetries, which is a crystalline symmetry, not an internal symmetry. Hence, this classification scheme is insufficient to describe this set of topological indices.

Topological Crystalline Insulators

In contrast, TCIs rely on the presence of certain crystal symmetries. TCIs are a cousin to topological insulators. It has been noticed that materials made out of chemically similar elements arranged in same crystal structure have similar electronic properties.

• e.g. Si, Ge, and Diamond all made of group 4 elements and have same crystal structure. All three are insulators with band gap of order of 1 eV

Question: Are there topologically distinct states with the same crystal structure? Are there topologically non-trivial states protected by crystal symmetry instead of TRS?

The answer is yes.

Mirror TCIs

In 2008, Teo, Fu, and Kane showed that symmetry eigenvalues of the Bloch eigenstates at high-symmetry crystal momenta can reveal additional topological structure in inversion-symmetric topological insulators. They introduced a class of mirror-symmetric TCIs, including bismuth antimony, where a mirror symmetry leads to the mirror Chern number $n_{\mathcal{M}}$. In bismuth antimony, ${\mathcal{M}}_x$ symmetry labels states in the $k_x=0$ plane by their symmetry eigenvalues $\pm i$, allowing the Hamiltonian to block-diagonalize into two sectors $H_{\pm }$ with their own Chern numbers. Time-reversal symmetry guarantees that the total Chern number is zero, but the mirror Chern number

$$n_{\mathcal{M}}=(n_{+}-n_{-})/2$$

captures their difference and determines how the $\pm i$ irreps cross the Fermi level in the surface band structure along $k_x=0$. If $n_{+}=1$, the $+i$ irrep connects the valence and conduction bands, and similarly for $n_{-}$. This also specifies how many surface Dirac points are present, information absent in the ${\mathbb{Z}}_2$ classification.

$C_4$ TCIs

The concept of TCIs was introduced by Liang Fu in 2011. In this paper, he used a tight-binding Hamiltonian of $p_x$ and $p_y$ orbitals on a lattice with $C_4$ rotational symmetry and time-reversal symmetry ($\mathcal{T}$). Surfaces that respect this symmetry in specific parameter regimes have states crossing the Fermi energy while the bulk remains gapped.

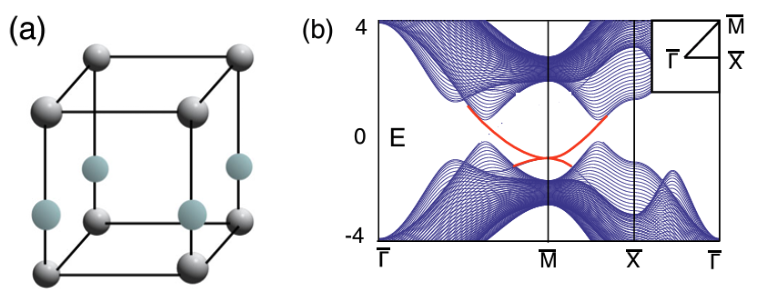
As shown in the figure above, these states have a quadratic touching at the $C_4$ invariant high-symmetry momentum (HSM) $\bar{M}=(\pi ,\pi )$, differing from the linear Dirac dispersion at time-reversal invariant (TRIM) momenta in ${\mathbb{Z}}_2$ topological insulators. This band crossing is topologically protected in the presence of $C_4$ and $\mathcal{T}$; however, when adding $C_4$ or $\mathcal{T}$ symmetry-breaking terms to the Hamiltonian, the crossing becomes gapped, and the system is trivial.

Fu derives a bulk-defined topological ${\mathbb{Z}}_2$ invariant in the paper, analogous to that of a spin-Hall ${\mathbb{Z}}_2$ insulator. It involves the Pffafian of an antisymmetric unitary overlap matrix $W_{m,n}({\mathbf{k}}_i)=⟨u_{m{\mathbf{k}}_i}|C_4\mathcal{T}|u_{n{\mathbf{k}}_i}⟩$ defined at the $C_4$ and $\mathcal{T}$ invariant HSM; $\Gamma =(0,0,0)$, $M=(\pi ,\pi ,0)$, $A=(\pi ,\pi ,\pi )$, and $Z=(0,0,\pi )$. This invariant depends closely on the symmetry of the crystal. When $\mathcal{T}$ and $C_4$ are symmetries, this leads to protected degeneracies at the four invariant HSM. At these points, the energy bands are eigenstates of the $C_4$ operator with eigenvalues $1,-1,+i,-i$. Without spin-orbit coupling and with $\mathcal{T}$ symmetry, the $\pm i$ eigenstates are doubly degenerate, forming a two-dimensional irreducible representation (irrep) of the symmetry group. The ${\mathbb{Z}}_2$ invariant is only well-defined for these doublets, which can be understood mathematically as the constraint of needing an anti-symmetric overlap matrix $W$ for the Pfaffian to be well-defined, only being possible even dimensional matrices, or physically from the fact that symmetry can only protect degenerate surface band crossings for doublets, not singlets. This illustrates the interplay of symmetry and topology in TCIs.

Tin Telluride: First TCI

In 2012 first realization of topological crystalline insulators found in Tin Telluride (SnTe), a binary compound with rocksalt crystal structure. Conversely, lead telluride is non-topological with same crystal structure.

Tin telluride is predicted to have topologically protected surface states while lead telluride does not; the topological protection comes from the mirror symmetry. Experimental groups observed surface states in tin telluride. These surface states open a band gap upon a structural distortion that breaks the mirror symmetry.

Summary: TCIs have topological surface states that are protected by crystal symmetries.

References

• YouTube link to Jennifer Cano’s Talk
• YouTube link to Liang Fu’s Talk