Planck's Quantum Resonators

References

• “Modern Physics”, Serway

Planck was convinced that blackbody radiation was produced by vibrating submicroscopic electrical charges he called resonators. He assumed the walls of a glowing cavity were composed of literally billions of these resonators, all vibrating at different frequencies. Hence, according to Maxwell, each oscillator should emit radiation at a frequency corresponding to its vibration frequency. Also, according to Maxwellian theory, an oscillator of frequency $f$ could have any value of energy and could change its amplitude continuously as it radiated any fraction of its energy.

This is where Planck made his revolutionary proposal. To secure agreement with experiment, Planck had to assume that the total energy of a resonator with mechanical frequency $f$ could only be integer multiples of $hf$.

$$E_{resonator}=nhfn=1,2,3,\cdots$$

In addition, he concluded that emission of frequency f occurred when a resonator dropped to the next lowest energy state. Thus the resonator can change its energy only by the difference $\Delta E$ according to

$$\Delta E=hf$$

it cannot lose just any amount of energy, only a finite amount, $hf$, the so called quantum of energy.

Until now we have been discussing single quantum oscillators of frequency $f$. Planck explained the continuous nature of blackbodies by assuming the heated walls contained resonators vibrating at many different frequencies, each emitting light at the same frequency of its vibration. By considering the conditions leading to equilibrium between the wall resonators and the radiation in the cavity, he was able to show that the spectral energy density $u(f,T)$ could be expressed as the product of the number of oscillators having frequency between $f$ and $f+df$, denoted by $N(f)df$, and the average energy emitted per oscillator.

$$u(f,T)df=\bar{E}N(f)df$$

Furthermore Planck showed that the number of oscillators with frequency between $f$ and $f+df$ is proportional to $f^2$

$$N(f)df=\frac{8\pi f^2}{c^3}df$$ $$u(f,T)df=\bar{E}\frac{8\pi f^2}{c^3}df$$

The result shows that the spectral energy density is proportional to the product of the frequency squared and the average energy of the oscillator. Also, since $u(f,T)$ approaches zero at high frequencies, $\bar{E}$ must tend to zero at frequencies faster than $\frac{1}{f^2}$. The fact that the mean oscillator energy must become extremely small at high frequencies guided Planck in the development of his theory. We shall see that the failure of $\bar{E}$ to become small at high frequencies in the classical Raleigh-Jeans theory led to the “Ultraviolet Catastrophe”.

Example: Classical versus Quantum Oscillators

Consider the implications of Planck’s conjecture that all oscillating systems of natural frequency f have discrete allowed energies $E=nhf$ and that the smallest change in energy of the system is $\Delta E=hf$.

a First compare an atomic oscillator sending out 540-nm light (green) to one sending out 700-nm light (red) by calculating the minimum energy change in each. For the green quantum,

$$\Delta E_{Green}=hf=\frac{hc}{\lambda }=\frac{(6.626\times 10^{-34}\mathrm{J}\cdot \mathrm{s})(3.00\times 10^{8}m/s)}{540\times 10^{-9}\mathrm{m}}$$

$\Delta E_{Green}=3.68\times 10^{-19}\mathrm{J}$ Using eV (electron Volts) here is much more appropriate. By definition it is the energy gained by an electron accelerated through a potential difference of 1 V. $1\mathrm{eV}=V\cdot q=(1.602\times 10^{-19}\mathrm{C})(1J/C)=1.602\times 10^{-19}\mathrm{J}$. Also, $h=4.136\times 10^{-15}\mathrm{eV}\cdot \mathrm{s}$. So

$$\Delta E_{Green}=\frac{3.68\times 10^{-19}\mathrm{J}}{1.602\times 10^{-19}J/eV}=2.30\mathrm{eV}$$

For the red quantum,

$$\Delta E_{Red}=\frac{hc}{\lambda }=\frac{(6.626\times 10^{-34}\mathrm{J}\cdot \mathrm{s})(3.00\times 10^{8}m/s)}{700\times 10^{-9}\mathrm{m}}$$

$\Delta E_{Red}=2.84\times 10^{-19}\mathrm{J}=1.77\mathrm{J}$

Rayleigh Jeans Law

Both Planck and Raleigh Jeans laws may be derived from the idea that the blackbody radiation energy per unit volume with frequency between $f$ and $f+df$ can be expressed as a product of the number of oscillators per unit volume in this frequency range and the average energy per oscillator:

$$u(f,T)df=\bar{E}N(f)df$$

It is instructive to perform both the Rayleigh–Jeans and Planck calculations to see the effect on $u(f,T)$ of calculating E from a continuous distribution of classical oscillator energies (Rayleigh–Jeans) as opposed to a discrete set of quantum oscillator energies (Planck). While Planck concentrated on the thermal equilibrium of cavity radiation with oscillating electric charges in the cavity walls, Rayleigh concentrated directly on the electromagnetic waves in the cavity. Rayleigh and Jeans reasoned that the standing electromagnetic waves in the cavity could be considered to have a temperature T, because they constantly ex- changed energy with the walls and caused a thermometer within the cavity to reach the same temperature as the walls. Further, they considered a standing polarized electromagnetic wave to be equivalent to a one-dimensional oscillator. Using the same general idea as Planck, they expressed the energy density as a product of the number of standing waves (oscillators) and the average energy per oscillator. They found the average oscillator energy E to be independent of frequency and equal to $k_{B}T$ from the Maxwell-Boltzmann distribution law. According to this distribution law, the probability P of finding an individual system (such as a molecule or an atomic oscillator) with energy E above some minimum energy, $E_0$, in a large group of systems at temperature T is:

$$P(E)=P_0{e}^{-(E-E_0)/k_{B}T}$$

where $P_0$ is the probability that the system has the minimum energy. In the case of a discrete set of allowed energies, the average energy $\bar{E}$ is given by $\bar{E}=\frac{\sum E\cdot P(E)}{\sum P(E)}$ In the classical case considered by Rayleigh, an oscillator could have any energy E in the continuous range from 0 to $\infty$. In the classical case, the sums must be replaced with integrals.

$$\bar{E}=\frac{{\int }_0^{\infty }E{e}^{-E/k_{b}T}dE}{{\int }_0^{\infty }{e}^{-E/k_{b}T}dE}=k_{B}T$$

The calculation of N(f) is a bit more complicated but is of importance here as well as in the free electron model of metals. After derivation of the density of modes one finds

$$N(f)df=\frac{8\pi f^2}{c^3}df$$

or in terms of wavelength

$$N(\lambda )d\lambda =\frac{8\pi }{{\lambda }^4}d\lambda$$

The spectral energy density is simply the density of modes multiplied by $k_{B}T$.

$$u(f,T)df=\frac{8\pi f^2}{c^3}{k}_{B}Tdf$$

In terms of wavelength

$$u(\lambda ,T)d\lambda =\frac{8\pi }{{\lambda }^4}{k}_{B}Td\lambda$$

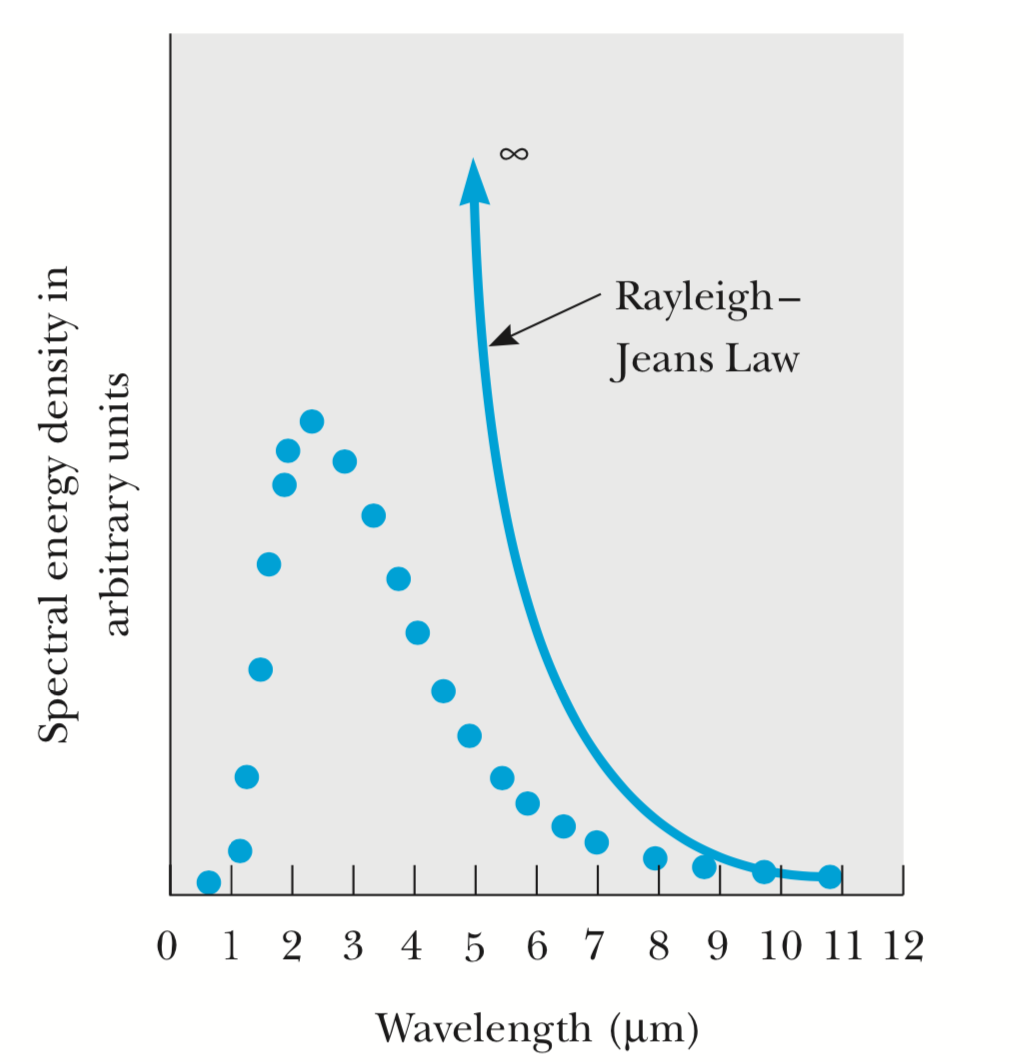
As can be seen in figure 3, this classical expression, known as the Rayleigh–Jeans law, does not agree with the experimental results in the short wavelength region. One is forced to conclude that classical theory fails miserably to explain blackbody radiation.

Planck’s Law

Planck concentrated on the energy states of resonators in the cavity walls and used the condition that the resonators and cavity radiation were in equilibrium to determine the spectral quality of the radiation. By thermodynamic reasoning (and apparently unaware of Rayleigh’s derivation), he arrived at the same expression for $N(f)$ as Rayleigh. However, Planck arrived at a different form for $\bar{E}$ by allowing only discrete values of energy for his resonators. He found, using the Maxwell-Boltzmann distribution law, $\bar{E}=\frac{hf}{e^{hf/k_{B}T}-1}$ Multiplying $\bar{E}$ by N(f) gives the Planck distribution formula: $u(f,T)df=\frac{8\pi f^2}{c^3}(\frac{hf}{e^{hf/k_{B}T}-1})df$ This shows that the ultraviolet catastrophe is avoided because the $\bar{E}$ term dominates the $f^2$ term at high frequencies. One can qualitatively understand why $\bar{E}$ tends to zero at high frequencies by noting that the first allowed oscillator level $hf$ is so large for large $f$ compared to the average thermal energy available $k_{B}T$ that Boltzmann’s law predicts almost zero probability that the first excited state is occupied.

In summary, Planck arrived at his blackbody formula by making two startling assumptions:

1. the energy of a charged oscillator of frequency $f$ is limited to discrete values $nhf$ and
2. During emission or absorption of light, the change in energy of an oscillator is $hf$.

From most of Planck’s early correspondence one gets the impression that his concept of energy quantization was really a desperate calculational device, and moreover a device that applied only in the case of blackbody radiation. It remained for Albert Einstein to elevate quantization to the level of a universal phenomenon by showing that light itself was quantized.